DESCRIPCIÓN DE LA GEOMETRÍA
Geometría de iluminación
La posición relativa del sol respecto de la superficie terrestre está completamente determinada por la geometría de iluminación. Los ángulos involucrados en este caso son el cenital solar (q0), y el azimutal solar (f0).
El ángulo cenital solar representa la posición del sol relativa a la normal local. Toma valores de 0º a 90º y se calcula con la siguiente ecuación:
![]()
donde j, d y h son la latitud, la declinación solar y el ángulo horario respectivamente.
El ángulo azimutal solar f0 es el ángulo determinado por la proyección de la posición del sol sobre la superficie de la tierra. Varía desde 0º a 360º y se calcula mediante las siguientes ecuaciones:
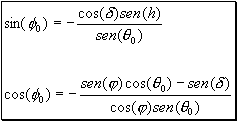
El signo menos en estas expresiones se corresponde con la Convención del Hemisferio Sur para las mediciones de ángulos. Así, en el caso del Hemisferio Norte, al ángulo azimutal se mide desde el Sur hacia el Este, y por lo tanto estas ecuaciones tienen un signo + en lugar de – delante de cada ecuación.
La Figura 1 muestra las diferentes configuraciones geométricas. La Figura 1(a) representa la geometría esférica para un píxel occidental, cuyo punto de observación es Pw , fijo a la superficie de la tierra. Figuras 1(b) y (c) representan los planos azimutales de observación para un píxel occidental y oriental respectivamente, según los modos de operación Mas y Mds (ascendente y descendente). El primero es el caso real de una escena iluminada por el sol por la tarde, y el segundo es el caso real de una escena matutina iluminada por el sol. Queda implícita la dependencia de los ángulos con la posición del píxel. Observación: El subíndice cero usado en las variables indica que las mismas se consideran en la dirección de iluminación.
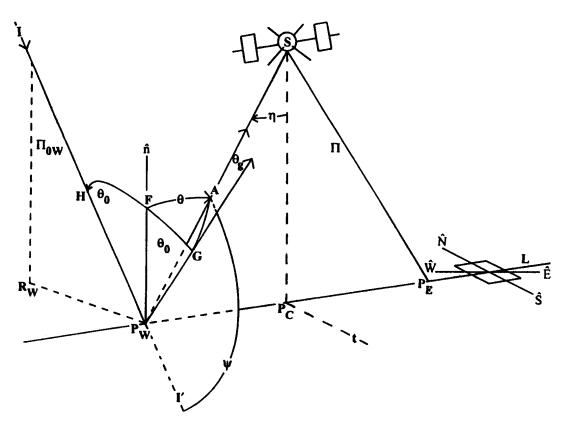
Figura 1 (a): Geometría esférica para un píxel occidental
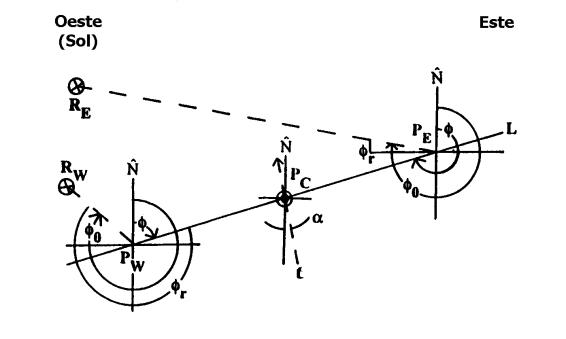
Figura 1 (b): Plano azimutal de observación para un píxel occidental
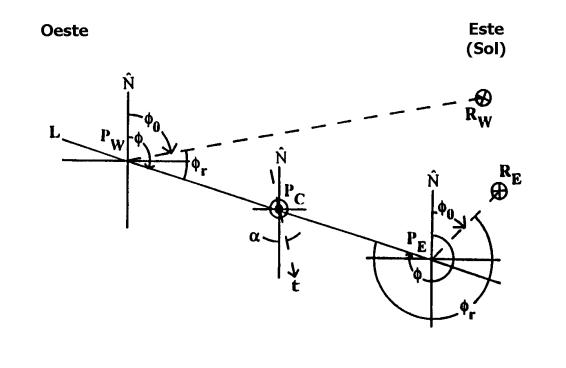
Figura 1 (c): Plano azimutal de observación para un píxel oriental
Geometría de observación
La posición relativa del sensor respecto de la superficie de la tierra queda completamente determinada por la geometría de observación. Los ángulos involucrados en este caso son el cenital del sensor y azimutal del sensor.
El ángulo cenital del sensor q representa la posición del satélite relativa a la normal y viene dado por la siguiente fórmula:
![]()
donde h [km] es la altitud del sensor, RT [km] es el radio terrestre y h es el ángulo de barrido. El factor (1+ h/RT) da cuenta de la curvatura de la Tierra, suponiendo, por simplicidad, una órbita circular del sensor.
El ángulo azimutal del sensor f está determinado por la proyección de la posición del sensor sobre la superficie de la tierra, según las siguientes fórmulas:
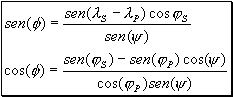
donde jS y lS son la latitud y longitud del punto sub-satelital, y jP y lp son la latitud y longitud del píxel observado sobre la línea de barrido.
Combinación de las geometrías de observación e iluminación
Combinando las geometrías de iluminación y de observación, se obtienen otros ángulos de importancia para la teledetección, como por ejemplo el ángulo de scattering Y y el ángulo de glint qg .
El ángulo de scattering Y se define entre la dirección incidente y la dirección de observación, variando de 0º a 180º y dado por la fórmula:
![]()
donde m =cos(q ) y fr es el ángulo azimutal relativo, definido por la posición del sensor con respecto a la posición del sol, ambos proyectados en la superficie terrestre.
El ángulo de glint qg queda definido por:
![]()
![]()